What your results mean

Scores

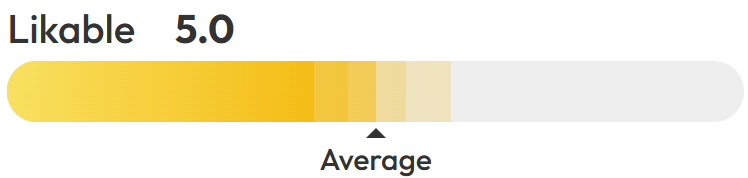
Photofeeler scores are given as a number between 1 and 10.

Your score takes into account the voting style of each person who gave you feedback (e.g. if they typically vote higher or lower for that trait and by how much).

Your scores are standardized so that you can easily compare your results to the general population. That is, a score of 5 is neither good nor bad, just average, as compared to photos typically found on Tinder, LinkedIn, or Facebook — accounting for the photo subject's gender and age.

If you hover or tap on one of the faded sections on the bars, a tooltip will tell you your current score's confidence intervals.

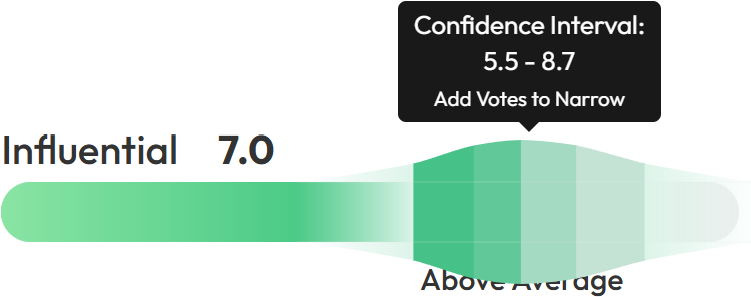
A confidence interval is a mathematical term, meaning the range in which Photofeeler is fairly certain your "true" score lies. (That is, the score your photo would end up with if you had thousands of votes.)

The more votes you add to your test, the smaller these ranges get.

Note: Photo tests with very split opinions will have wider confidence intervals and require more votes to obtain the same certainty.

Data

In Data mode, you may notice dark-colored notches in the bars.

If you hover or tap on any individual notch, a tooltip will tell you precisely what it means.

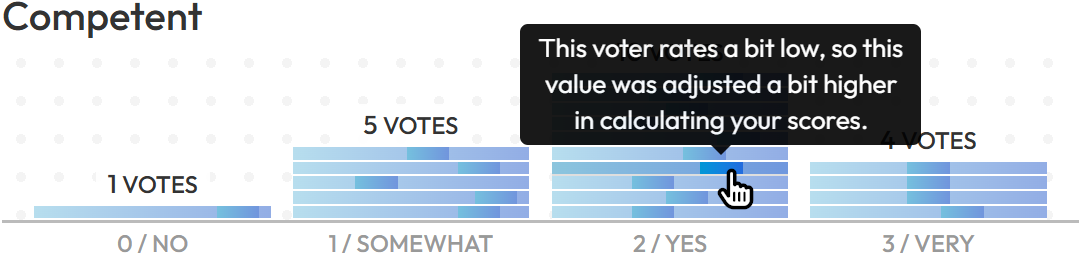
Generally, though, these notches represent the voting style of the person behind the vote and how that vote was adjusted in calculating your score.

For instance, if someone voted 3 ("very"), but consistently rates photos high for that trait, you'll see a notch on the far left of the bar. That means their "very" doesn't raise your score as much as the "very" of a person who rarely leaves 3s for that trait. Make sense?

Remember— We do we throw out poor-quality votes, so any votes that show up here have already met our standards of quality. So even if a voter is said to typically rate "very low" or "very high," we are confident that their votes are honest and careful, and they're not simply giving the same ratings again and again.

What makes a "good" score

A score of 5 is neither good nor bad, just average, as compared to photos of people your same gender and age.

Below that is below average; above that is above average.

Keep in mind that you could get an Attractive score of 1 for one photo and an Attractive score of 9 for another. Photofeeler cannot score you as a person. (Photofeeler tests photos, not people.)

What does "Quality Rough" mean?

This relates to the number of votes on the test so far.

If you have very few votes, the test is considered "rough" because it's not statistically significant yet.

Think of it like this: Imagine if you asked 5 random kids at an elementary school what pizza toppings they like. By coincidence, you could get 5 kids who like pineapple. That doesn't mean the whole school likes pineapple. You'd have to get a lot more opinions in order to separate the anomalies from the norm.

Our algorithms do speed this process significantly, so you can get an accurate score with a lot fewer scores than you'd need "in the real world," but a certain threshold of votes is still needed - as shown by that "Rough" indicator.

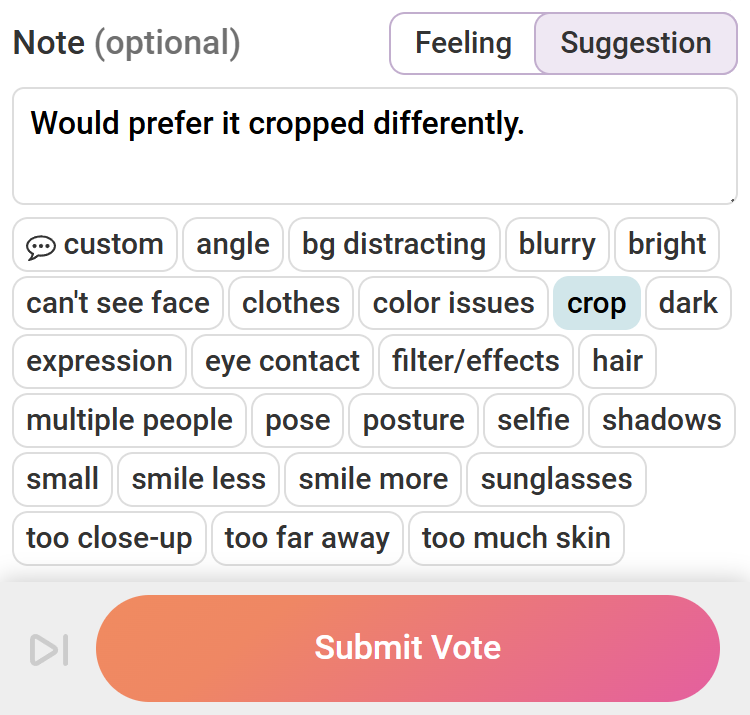
Repeats of the same Note

Don't worry, these Notes are not from the same person or from bots. Rather, these are Quick Notes (see below).

Oftentimes, different voters will send the same Quick Note, resulting in what looks like repeats. These Notes were picked out and sent by different people. When you get repeat notes, take this into consideration, as more than one person thinks similar thoughts about your photo.

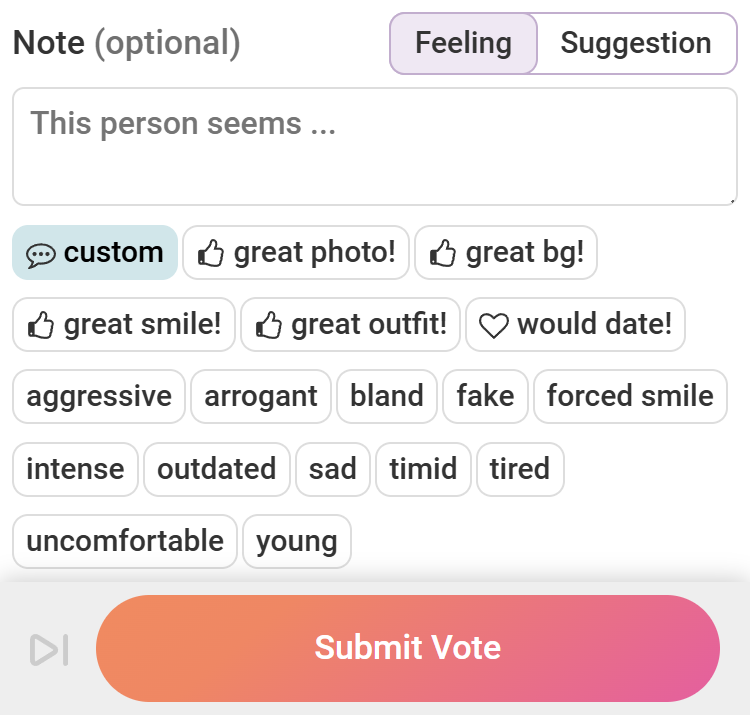
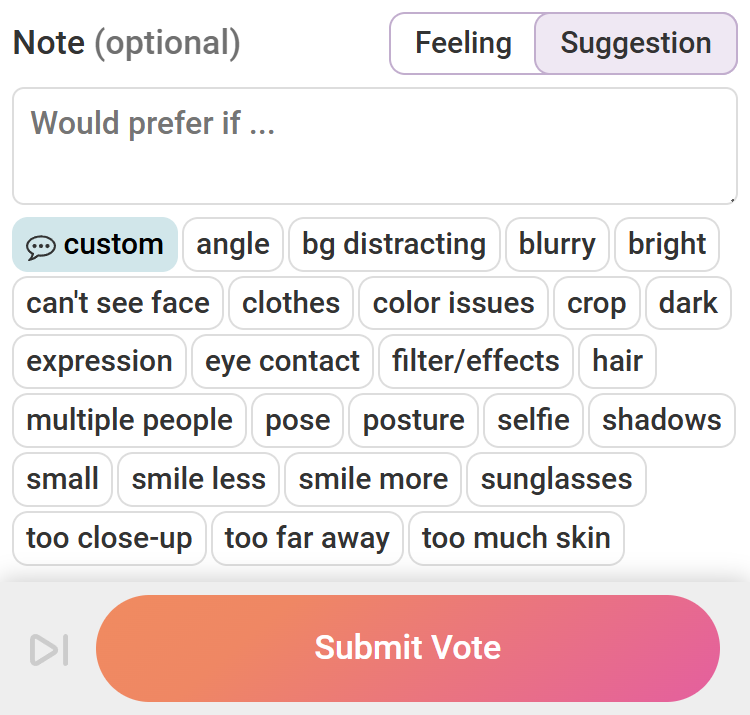
Quick Notes

Quick Notes are pre-written Notes available to voters on the voting page, just above the big, orange "Submit Vote" button.

We have found that most voters give better feedback by carefully picking out a Quick Note than when trying to come up with a critique on their own.

And thanks to Quick Notes, voters leave 10x as many Notes.

For more information and tips for improving your photos based on Quick Notes, see:

• What Common Notes on Photofeeler *Really* Mean
• How to fix "I think they seem a bit young in this photo"
• How to fix "I think they seem a bit intense in this photo"
• How to fix "Photo seems a bit artificial to me"
• How to fix "Photo seems a bit outdated to me"
• How to fix "Would prefer if it weren't so dark"
• How to fix "Would prefer if it weren't so bright"
• How to fix "Would prefer it without the shadows"
• How to fix "Would prefer a less distracting background"
• How to fix "Would prefer a different expression"
• How to fix "Would prefer less skin showing"
• How to fix "Would prefer if it didn't seem like a selfie"